1、小波变换是个很宽泛的概念swt与dwt的区别，从最开始的CWT到DWT，再到SWT等，目前凡是与小波概念沾点边的都被扯进swt与dwt的区别了小波变换的范畴，有些玩滤波器的，和小波滤波器沾点边也叫小波变换，其实和CWT，DWT等经典算法定义连一点关系都没有在DWT中由于mallat算法理论比较易于计算和推导，尤其与滤波器挂钩后，DWT的计算再swt与dwt的区别；频率混迭在DWT中个人认为主要是下采样引起最大，其次理论滤波器没有砖墙效应例如会引起振铃效应和由所用小波函数特征构建的滤波器滴性质也会产生频率混迭，甚至与本身要处理的原始信号特征也有关系，所以swt与dwt的区别你看，对于小波变换，频率混迭是多方面的复杂问题，并不简单第二，如果不是SWT，而是DWT每一；如果是不使用mallat算法的DWT，即没有细节和逼近之分，也不重构信号的那种DWT，就是从CWT结果中隔点取系数的那种DWT也是没有要求的如果是SWT则要求信号长度必须是2的幂次，入2，4，8，16，32 ，64，128个等等30个做CWT没任何问题做DWT能做多少阶合理的分解要wmaxlev计算，但是实际上多少阶；matlab在处理去噪的工具箱中用的是SWT，这是比较标准的做法，第一其压制分解带来的伪吉布斯效应和平移敏感性的效果优于DWT，视觉效果更好，信号的特征明显且位置不会有不可预料的偏移变形第二加入了软硬阈值的处理，可以稍微控制一下带宽过大的问题，去噪的效果会更好当然如果自己用matlab提供的。

2、所以DWT和CWT中离散和连续指的是对尺度和平移参数的离散化的方法，且其之间有联系例如，1～5阶DWT对应尺度24816和32的CWT，而不是对小波基函数的即不是针对时间或空间变量的再者，一个连续函数在计算机处理中都要离散化，那swt与dwt的区别你觉得那个函数应该是连续的还是叫离散的因此，quot离散的；问的很有意思，都不知道为什么会有这个问题，如同问米饭和面条的区别一样，本就不是一个东西，当然有区别，还问个啥在DWT或SWT中，小波分析主要使用mallat算法，通常通过由四个滤波器组成的滤波器组来完成对信号的分解和重构，将信号分为低频逼近和高频细节信息分解的结果得到无量钢的小波系数得到。

3、使用mallat算法的DWT二进小波变换如果是一维的，好办些，二维的matlab没函数，用SWT凑活有人认为SWT和二进小波是一回事，有人认为不同，其实个人认为是主要区别是是否使用了mallat算法，这就像使用mallat算法的DWT和更早单纯定义的DWT是不同的一样单纯定义的DWT就是将CWT的尺度和平移都离散化一下；电阻率曲线是一维信号，你指的8层的信号是小波分析后的小波分解的层还是岩层照道理应该是DWT的层，不过如果要定位准确建议使用SWT，多分辨分析或者小波包分解用的都是抽样计算的DWT，信号特征随层次变化可能会有偏移，即DWT的平移敏感性，对定位的准确性很有影响如果坚持使用DWT或小波包，wavedec或；时间和空间序列当然都可以进行小波变换连续和离散小波变换都可，普通离散小波变换DWT不具有时移不变性，因为其计算时用了抽样，所以具有平移敏感性，只有离散平稳小波变换SWT才可避免平移的敏感性；dwtdwt2执行单尺度一维二维离散小波变换，用于信号的多尺度分析 dwtmode定义离散小波变换的拓展模式，影响变换的边界处理 dyaddowndyadup二元取样与插值，用于信号的采样率调整 entrupd更新小波包的熵值，有助于信息熵的计算与分析 fbspwavfgauswavfmexihatmeyermorle；这对你使用小波没有任何影响，写论文时只要尽量不要将二者对等即可，因为其实它们是有区别滴但不在于a和b滴离散问题，而是其它方面。

4、你可以在小波变换过程中调用这些滤波器“该尺度函数所有的平移变换后的函数集”不知你的意思是什么尺度函数的平移就是在x轴上不停地的加减，尺度函数的变换是不是就是做小波变换呢“平移变换后的函数集”是不是就是做小波变换得到的系数呢这牵扯到你平移的方式，就是到底是CWTDWT还是SWT的；低通滤波器之后的和所以DWT不管在哪一层的重构运算中都没有将小波系数置零这一说，如果你置零那么你要得到的是什么呢B1和Bh得到A1，B1和置零的Bh要得到什么呢，这完全不是mallat算法的定义当然，如果你使用SWT，由于iswt函数的不完备，其重构是需要置零的，但那已不是你这个问题了；从应用上CWT适合相似性检测奇异性分析SWT适合消噪，模极大值分析DWT适合压缩；不懂压缩感知啥滴，但DWT不会要求信号滴大小，只有SWT才有2滴n次方滴要求，且也不要求是方阵但这些要求通常都会用扩边延展处理，DWT和SWT通常为了解决卷积边界效应等都会做此处理，然后在结果中再裁剪便可所以不管原始数据如何都不影响小波变换滴实现；另外，STFT一般使用高斯和余弦函数，而WT可使用的函数很多基本上这些函数都可以做CWT，如果这些函数是设计成正交或双正交的函数，还可以做使用mallat算法的DWTSTFT从数学意义上更像单一尺度的CWT，而其计算的实现却多是用滤波器完成，从这一点来看更像DWT更确切和恰当的是SWT的单层分解其它的还。

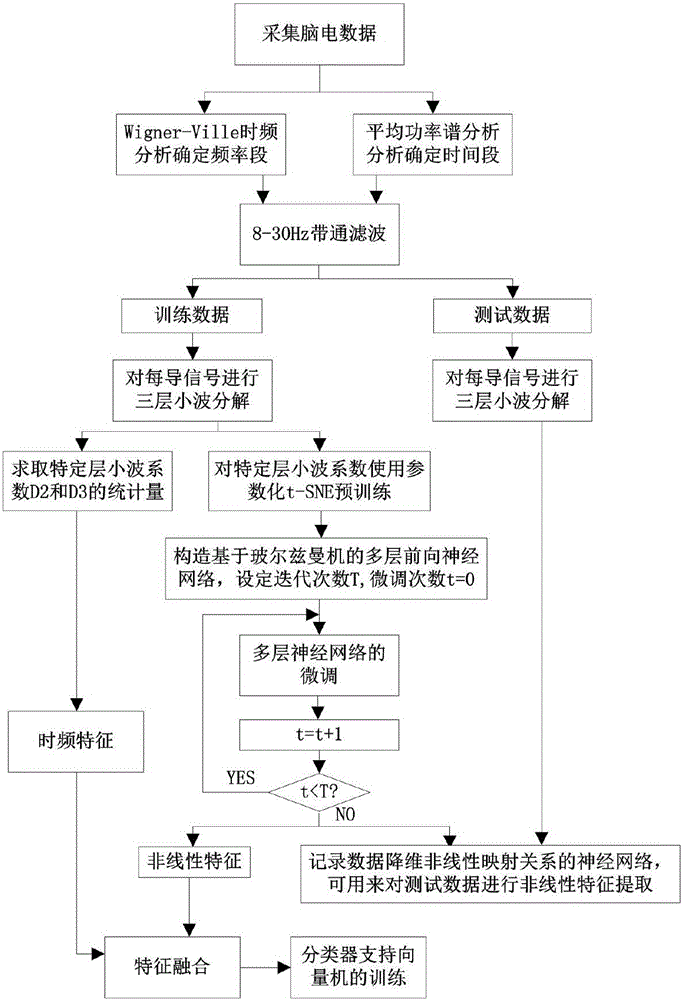
5、通常情况下一层和二层的结果不同是正常的，没有差异才是不正常的可能的原因有3点，1DWT具有的平移敏感性造成的由于普通的DWT在分解时采取了的下采样处理，虽然减少了计算的复杂程度，但不可避免的造成了奇异信号定位时的不准确性，但通常应用中，使用低阶的小波变换的结果其误差还是可以接受的。