方差标准差协方差相关系数是统计学中用于描述数据离散程度和相关性的关键概念在下文方差和协方差的区别，我们将详细阐述这些概念的定义计算公式以及它们之间的区别方差与标准差用于描述一组数据的离散程度方差是衡量每一个变量观察值与总体均数之间差异的统计量公式为方差 = 平方和除以样本数量标准差。

VarZ = a^2 * VarX + b^2 * VarY + 2ab * CovX， Y其中，VarZ 表示线性组合 Z 的方差a 和 b 是常数，表示线性组合中每个随机变量的系数VarX 和 VarY 分别表示随机变量 X 和 Y 的方差CovX， Y 表示随机变量 X 和 Y 的协方差协方差 CovX， Y。

则X和Y必不是相互独立的，亦即它们之间存在着一定的关系定义EXEXYEY称为随机变量X和Y的协方差，记作COVX，Y，即COVX，Y=EXEXYEY协方差与方差之间有如下关系DX+Y=DX+DY+2COVX，Y因此，COVX，Y=EXYEXE。

方差是用来衡量数据分布离散度的一个重要指标，具体而言，它表示的是样本值与其平均值偏离程度的平方平均值，反映方差和协方差的区别了数据的波动情况协方差则是一种衡量两个变量之间线性关系强度的统计量，它描述方差和协方差的区别了两个变量之间变化方向的一致性如果两个变量的协方差为正，则表明这两个变量倾向于同向变化反之，如果协。

值得注意的是，协方差仅能告诉我们变量间是否有关联及关联的方向性，并不能确定它们之间的因果关系若两个变量相互独立，那么它们的协方差为零在实际工作中，我们经常遇到多个变量的数据处理和分析问题，方差和协方差的区别了解每个变量的离散程度及各变量之间的关系是非常重要的因此，方差和协方差作为基础的统计量，在。

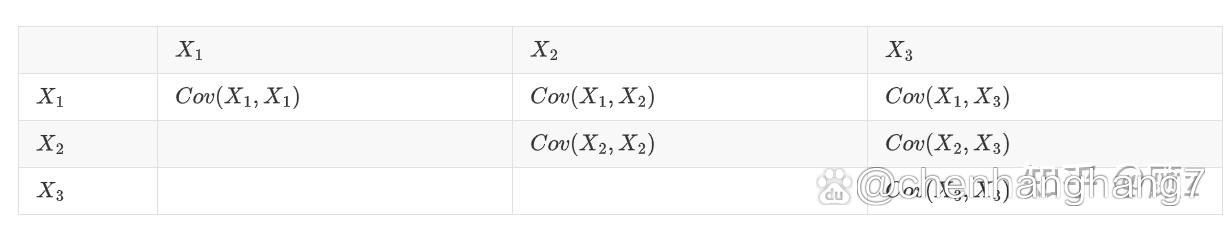
举例来说，一个数据集如果存在较大的方差，说明数据点之间的离散程度较大，可能存在异常值或较大的波动而较小的方差则表明数据点相对集中在一个较小的范围内波动较小在统计学分析中，方差常用于判断数据的稳定性和可靠性总的来说，协方差和方差都是数据分析中非常重要的统计量它们分别用于描述。

两者之间有以下关系1方差描述了数据点与平均值之间的离散程度，而协方差则描述了两个数据点之间的离散程度2方差是协方差的一种特殊情况，当两个数据点完全一样或者说它们之间没有任何关系时，它们的协方差就等于它们的方差3对于一组数据，方差和协方差都是衡量数据变异性的重要指标，但。

如果从计算来看，独立样本之间不需要进行计算，只在本组中进行计算均值标准差等，而方差分析中，要计算数据之间的组间差异和组内差异等另外，多因素方差分析就是分析多种因素对某一变量的影响有多大的检验分析而协方差分析是多种影响因素下，在不考虑某一种因素下，其方差和协方差的区别他因素对该变量的影响有多大。

首先，方差和标准差通常针对一维数据，也即各个数据描述的是同一类事物，比如身高标准差为方差的算术平方根方差和标准差用以刻画各个数据与所有数据平均值的靠近程度，它们的取值越小，则各数据同平均值越为接近其次，协方差针对二维数据，也即两个维度的数据描述的是不同类事物，比如身高和体重协。